Viterbi algorithm

Short description: Finds likely sequence of hidden states

The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events. This is done especially in the context of Markov information sources and hidden Markov models (HMM).

The algorithm has found universal application in decoding the convolutional codes used in both CDMA and GSM digital cellular, dial-up modems, satellite, deep-space communications, and 802.11 wireless LANs. It is now also commonly used in speech recognition, speech synthesis, diarization, keyword spotting, computational linguistics, and bioinformatics. For example, in speech-to-text (speech recognition), the acoustic signal is treated as the observed sequence of events, and a string of text is considered to be the "hidden cause" of the acoustic signal. The Viterbi algorithm finds the most likely string of text given the acoustic signal.

History

The Viterbi algorithm is named after Andrew Viterbi, who proposed it in 1967 as a decoding algorithm for convolutional codes over noisy digital communication links. It has, however, a history of multiple invention, with at least seven independent discoveries, including those by Viterbi, Needleman and Wunsch, and Wagner and Fischer. It was introduced to Natural Language Processing as a method of part-of-speech tagging as early as 1987.

Viterbi path and Viterbi algorithm have become standard terms for the application of dynamic programming algorithms to maximization problems involving probabilities. For example, in statistical parsing a dynamic programming algorithm can be used to discover the single most likely context-free derivation (parse) of a string, which is commonly called the "Viterbi parse". Another application is in target tracking, where the track is computed that assigns a maximum likelihood to a sequence of observations.

Extensions

A generalization of the Viterbi algorithm, termed the max-sum algorithm (or max-product algorithm) can be used to find the most likely assignment of all or some subset of latent variables in a large number of graphical models, e.g. Bayesian networks, Markov random fields and conditional random fields. The latent variables need, in general, to be connected in a way somewhat similar to a hidden Markov model (HMM), with a limited number of connections between variables and some type of linear structure among the variables. The general algorithm involves message passing and is substantially similar to the belief propagation algorithm (which is the generalization of the forward-backward algorithm).

With the algorithm called iterative Viterbi decoding one can find the subsequence of an observation that matches best (on average) to a given hidden Markov model. This algorithm is proposed by Qi Wang et al. to deal with turbo code. Iterative Viterbi decoding works by iteratively invoking a modified Viterbi algorithm, reestimating the score for a filler until convergence.

An alternative algorithm, the Lazy Viterbi algorithm, has been proposed. For many applications of practical interest, under reasonable noise conditions, the lazy decoder (using Lazy Viterbi algorithm) is much faster than the original Viterbi decoder (using Viterbi algorithm). While the original Viterbi algorithm calculates every node in the trellis of possible outcomes, the Lazy Viterbi algorithm maintains a prioritized list of nodes to evaluate in order, and the number of calculations required is typically fewer (and never more) than the ordinary Viterbi algorithm for the same result. However, it is not so easy to parallelize in hardware.

Pseudocode

This algorithm generates a path [math]\displaystyle{ X=(x_1,x_2,\ldots,x_T) }[/math], which is a sequence of states [math]\displaystyle{ x_n \in S=\{s_1,s_2,\dots,s_K\} }[/math] that generate the observations [math]\displaystyle{ Y=(y_1,y_2,\ldots, y_T) }[/math] with [math]\displaystyle{ y_n \in O=\{o_1,o_2,\dots,o_N\} }[/math], where [math]\displaystyle{ N }[/math] is the number of possible observations in the observation space [math]\displaystyle{ O }[/math].

Two 2-dimensional tables of size [math]\displaystyle{ K \times T }[/math] are constructed:

• Each element [math]\displaystyle{ T_1[i,j] }[/math] of [math]\displaystyle{ T_1 }[/math] stores the probability of the most likely path so far [math]\displaystyle{ \hat{X}=(\hat{x}_1,\hat{x}_2,\ldots,\hat{x}_j) }[/math] with [math]\displaystyle{ \hat{x}_j=s_i }[/math] that generates [math]\displaystyle{ Y=(y_1,y_2,\ldots, y_j) }[/math].
• Each element [math]\displaystyle{ T_2[i,j] }[/math] of [math]\displaystyle{ T_2 }[/math] stores [math]\displaystyle{ \hat{x}_{j-1} }[/math] of the most likely path so far [math]\displaystyle{ \hat{X}=(\hat{x}_1,\hat{x}_2,\ldots,\hat{x}_{j-1},\hat{x}_j = s_i) }[/math] [math]\displaystyle{ \forall j, 2\leq j \leq T }[/math]

The table entries [math]\displaystyle{ T_1[i,j],T_2[i,j] }[/math] are filled by increasing order of [math]\displaystyle{ K\cdot j+i }[/math]:

[math]\displaystyle{ T_1[i,j]=\max_{k}{(T_1[k,j-1]\cdot A_{ki}\cdot B_{iy_j})} }[/math],

[math]\displaystyle{ T_2[i,j]=\operatorname{argmax}_{k}{(T_1[k,j-1]\cdot A_{ki} \cdot B_{iy_j})} }[/math],

with [math]\displaystyle{ A_{ki} }[/math] and [math]\displaystyle{ B_{iy_j} }[/math] as defined below. Note that [math]\displaystyle{ B_{iy_j} }[/math] does not need to appear in the latter expression, as it's non-negative and independent of [math]\displaystyle{ k }[/math] and thus does not affect the argmax.

Input

• The observation space [math]\displaystyle{ O=\{o_1,o_2,\dots,o_N\} }[/math],
• the state space [math]\displaystyle{ S=\{s_1,s_2,\dots,s_K\} }[/math],
• an array of initial probabilities [math]\displaystyle{ \Pi = (\pi_1,\pi_2,\dots,\pi_K) }[/math] such that [math]\displaystyle{ \pi_i }[/math] stores the probability that [math]\displaystyle{ x_1 = s_i }[/math],
• a sequence of observations [math]\displaystyle{ Y=(y_1,y_2,\ldots, y_T) }[/math] such that [math]\displaystyle{ y_t=o_i }[/math] if the observation at time [math]\displaystyle{ t }[/math] is [math]\displaystyle{ o_i }[/math],
• transition matrix [math]\displaystyle{ A }[/math] of size [math]\displaystyle{ K\times K }[/math] such that [math]\displaystyle{ A_{ij} }[/math] stores the transition probability of transiting from state [math]\displaystyle{ s_i }[/math] to state [math]\displaystyle{ s_j }[/math],
• emission matrix [math]\displaystyle{ B }[/math] of size [math]\displaystyle{ K\times N }[/math] such that [math]\displaystyle{ B_{ij} }[/math] stores the probability of observing [math]\displaystyle{ o_j }[/math] from state [math]\displaystyle{ s_i }[/math].

Output

• The most likely hidden state sequence [math]\displaystyle{ X=(x_1,x_2,\ldots,x_T) }[/math]

function VITERBI[math]\displaystyle{ (O,S,\Pi,Y,A,B):X }[/math]
    for each state [math]\displaystyle{ i=1,2,\ldots,K }[/math] do
        [math]\displaystyle{ T_1[i,1]\leftarrow\pi_i\cdot B_{iy_1} }[/math]
        [math]\displaystyle{ T_2[i,1]\leftarrow  0 }[/math]
    end for
    for each observation [math]\displaystyle{ j = 2,3,\ldots,T }[/math] do
        for each state [math]\displaystyle{ i =1,2,\ldots,K }[/math] do
            [math]\displaystyle{ T_1[i,j] \gets \max_{k}{(T_1[k,j-1]\cdot A_{ki} \cdot B_{iy_j})}  }[/math]
            [math]\displaystyle{ T_2[i,j] \gets \arg\max_{k}{(T_1[k,j-1]\cdot A_{ki} \cdot B_{iy_j}) }  }[/math]
        end for
    end for
    [math]\displaystyle{ z_T \gets \arg\max_{k}{(T_1[k,T])}  }[/math]
    [math]\displaystyle{ x_T\leftarrow s_{z_T} }[/math]
    for [math]\displaystyle{ j=T,T-1,\ldots,2 }[/math] do
        [math]\displaystyle{ z_{j-1}\leftarrow T_2[z_j,j] }[/math]
        [math]\displaystyle{ x_{j-1}\leftarrow s_{z_{j-1}} }[/math]
    end for
    return [math]\displaystyle{ X }[/math]
end function

Restated in a succinct near-Python:

function viterbi[math]\displaystyle{ (O, S, \Pi, Tm, Em): best\_path }[/math]   Tm: transition matrix   Em: emission matrix
    [math]\displaystyle{ trellis \leftarrow matrix(length(S), length(O)) }[/math]      To hold probability of each state given each observation
    [math]\displaystyle{ pointers \leftarrow matrix(length(S), length(O)) }[/math]    To hold backpointer to best prior state
    for s in [math]\displaystyle{ range(length(S)) }[/math]:                Determine each hidden state's probability at time 0…
        [math]\displaystyle{ trellis[s, 0] \leftarrow \Pi[s] \cdot Em[s, O[0]] }[/math]
    for o in [math]\displaystyle{ range(1, length(O)) }[/math]:              …and after, tracking each state's most likely prior state, k
        for s in [math]\displaystyle{ range(length(S)) }[/math]:
            [math]\displaystyle{ k \leftarrow \arg\max(trellis[k, o-1] \cdot Tm[k, s] \cdot Em[s, o]\ \mathsf{for}\ k\ \mathsf{in}\ range(length(S))) }[/math]
            [math]\displaystyle{ trellis[s, o] \leftarrow trellis[k, o-1] \cdot Tm[k, s] \cdot Em[s, o] }[/math]
            [math]\displaystyle{ pointers[s, o] \leftarrow k }[/math]
    [math]\displaystyle{ best\_path \leftarrow list() }[/math]
    [math]\displaystyle{ k \leftarrow \arg\max(trellis[k, length(O)-1]\ \mathsf{for}\ k\ \mathsf{in}\ range(length(S))) }[/math]    Find k of best final state
    for o in [math]\displaystyle{ range(length(O)-1, -1, -1) }[/math]:      Backtrack from last observation
        [math]\displaystyle{ best\_path.insert(0, S[k]) }[/math]                Insert previous state on most likely path
        [math]\displaystyle{ k \leftarrow pointers[k, o] }[/math]                      Use backpointer to find best previous state
    return [math]\displaystyle{ best\_path }[/math]

Explanation

Suppose we are given a hidden Markov model (HMM) with state space [math]\displaystyle{ S }[/math], initial probabilities [math]\displaystyle{ \pi_i }[/math] of being in the hidden state [math]\displaystyle{ i }[/math] and transition probabilities [math]\displaystyle{ a_{i,j} }[/math] of transitioning from state [math]\displaystyle{ i }[/math] to state [math]\displaystyle{ j }[/math]. Say, we observe outputs [math]\displaystyle{ y_1,\dots, y_T }[/math]. The most likely state sequence [math]\displaystyle{ x_1,\dots,x_T }[/math] that produces the observations is given by the recurrence relations

[math]\displaystyle{ \begin{align} V_{1,k} &= \mathrm{P}\big( y_1 \ | \pi_k \big) \cdot \pi_k, \\ V_{t,k} &= \max_{x \in S} \left( \mathrm{P}\big( y_t \ | \pi_k \big) \cdot a_{x,k} \cdot V_{t-1,x}\right). \end{align} }[/math]

Here [math]\displaystyle{ V_{t,k} }[/math] is the probability of the most probable state sequence [math]\displaystyle{ \mathrm{P}\big(x_1,\dots,x_t,y_1,\dots, y_t\big) }[/math] responsible for the first [math]\displaystyle{ t }[/math] observations that have [math]\displaystyle{ k }[/math] as its final state. The Viterbi path can be retrieved by saving back pointers that remember which state [math]\displaystyle{ x }[/math] was used in the second equation. Let [math]\displaystyle{ \mathrm{Ptr}(k,t) }[/math] be the function that returns the value of [math]\displaystyle{ x }[/math] used to compute [math]\displaystyle{ V_{t,k} }[/math] if [math]\displaystyle{ t \gt 1 }[/math], or [math]\displaystyle{ k }[/math] if [math]\displaystyle{ t=1 }[/math]. Then

[math]\displaystyle{ \begin{align} x_T &= \arg\max_{x \in S} (V_{T,x}), \\ x_{t-1} &= \mathrm{Ptr}(x_t,t). \end{align} }[/math]

Here we're using the standard definition of arg max.

The complexity of this implementation is [math]\displaystyle{ O(T\times\left|{S}\right|^2) }[/math]. A better estimation exists if the maximum in the internal loop is instead found by iterating only over states that directly link to the current state (i.e. there is an edge from [math]\displaystyle{ k }[/math] to [math]\displaystyle{ j }[/math]). Then using amortized analysis one can show that the complexity is [math]\displaystyle{ O(T\times(\left|{S}\right| + \left|{E}\right|)) }[/math], where [math]\displaystyle{ E }[/math] is the number of edges in the graph.

Example

Consider a village where all villagers are either healthy or have a fever, and only the village doctor can determine whether each has a fever. The doctor diagnoses fever by asking patients how they feel. The villagers may only answer that they feel normal, dizzy, or cold.

The doctor believes that the health condition of the patients operates as a discrete Markov chain. There are two states, "Healthy" and "Fever", but the doctor cannot observe them directly; they are hidden from the doctor. On each day, there is a certain chance that a patient will tell the doctor "I feel normal", "I feel cold", or "I feel dizzy", depending on the patient's health condition.

The observations (normal, cold, dizzy) along with a hidden state (healthy, fever) form a hidden Markov model (HMM), and can be represented as follows in the Python programming language:

obs = ("normal", "cold", "dizzy")
states = ("Healthy", "Fever")
start_p = {"Healthy": 0.6, "Fever": 0.4}
trans_p = {
    "Healthy": {"Healthy": 0.7, "Fever": 0.3},
    "Fever": {"Healthy": 0.4, "Fever": 0.6},
}
emit_p = {
    "Healthy": {"normal": 0.5, "cold": 0.4, "dizzy": 0.1},
    "Fever": {"normal": 0.1, "cold": 0.3, "dizzy": 0.6},
}

In this piece of code, start_p represents the doctor's belief about which state the HMM is in when the patient first visits (all the doctor knows is that the patient tends to be healthy). The particular probability distribution used here is not the equilibrium one, which is (given the transition probabilities) approximately {'Healthy': 0.57, 'Fever': 0.43}. The transition_p represents the change of the health condition in the underlying Markov chain. In this example, a patient who is healthy today has only a 30% chance of having a fever tomorrow. The emit_p represents how likely each possible observation (normal, cold, or dizzy) is, given the underlying condition (healthy or fever). A patient who is healthy has a 50% chance of feeling normal; one who has a fever has a 60% chance of feeling dizzy.

Graphical representation of the given HMM

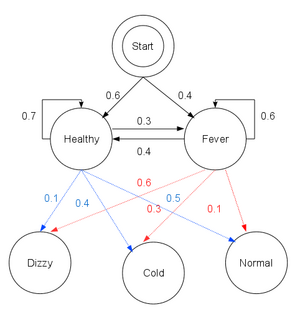
A patient visits three days in a row, and the doctor discovers that the patient feels normal on the first day, cold on the second day, and dizzy on the third day. The doctor has a question: what is the most likely sequence of health conditions of the patient that would explain these observations? This is answered by the Viterbi algorithm.

def viterbi(obs, states, start_p, trans_p, emit_p):
    V = [{}]
    for st in states:
        V[0] [st] = {"prob": start_p[st] * emit_p[st] [obs[0]], "prev": None}
    # Run Viterbi when t > 0
    for t in range(1, len(obs)):
        V.append({})
        for st in states:
            max_tr_prob = V[t - 1] [states[0]] ["prob"] * trans_p[states[0]] [st] * emit_p[st] [obs[t]]
            prev_st_selected = states[0]
            for prev_st in states[1:]:
                tr_prob = V[t - 1] [prev_st] ["prob"] * trans_p[prev_st] [st] * emit_p[st] [obs[t]]
                if tr_prob > max_tr_prob:
                    max_tr_prob = tr_prob
                    prev_st_selected = prev_st

            max_prob = max_tr_prob
            V[t] [st] = {"prob": max_prob, "prev": prev_st_selected}

    for line in dptable(V):
        print(line)

    opt = []
    max_prob = 0.0
    best_st = None
    # Get most probable state and its backtrack
    for st, data in V[-1].items():
        if data["prob"] > max_prob:
            max_prob = data["prob"]
            best_st = st
    opt.append(best_st)
    previous = best_st

    # Follow the backtrack till the first observation
    for t in range(len(V) - 2, -1, -1):
        opt.insert(0, V[t + 1] [previous] ["prev"])
        previous = V[t + 1] [previous] ["prev"]

    print ("The steps of states are " + " ".join(opt) + " with highest probability of %s" % max_prob)

def dptable(V):
    # Print a table of steps from dictionary
    yield " " * 5 + "     ".join(("%3d" % i) for i in range(len(V)))
    for state in V[0]:
        yield "%.7s: " % state + " ".join("%.7s" % ("%lf" % v[state] ["prob"]) for v in V)

The function viterbi takes the following arguments: obs is the sequence of observations, e.g. ['normal', 'cold', 'dizzy']; states is the set of hidden states; start_p is the start probability; trans_p are the transition probabilities; and emit_p are the emission probabilities. For simplicity of code, we assume that the observation sequence obs is non-empty and that trans_p[i] [j] and emit_p[i] [j] is defined for all states i,j.

In the running example, the forward/Viterbi algorithm is used as follows:

viterbi(obs,
        states,
        start_p,
        trans_p,
        emit_p)

The output of the script is

$ python viterbi_example.py
         0          1          2
Healthy: 0.30000 0.08400 0.00588
Fever: 0.04000 0.02700 0.01512
The steps of states are Healthy Healthy Fever with highest probability of 0.01512

This reveals that the observations ['normal', 'cold', 'dizzy'] were most likely generated by states ['Healthy', 'Healthy', 'Fever']. In other words, given the observed activities, the patient was most likely to have been healthy on the first day and also on the second day (despite feeling cold that day), and only to have contracted a fever on the third day.

The operation of Viterbi's algorithm can be visualized by means of a trellis diagram. The Viterbi path is essentially the shortest path through this trellis.

Soft output Viterbi algorithm

The soft output Viterbi algorithm (SOVA) is a variant of the classical Viterbi algorithm.

SOVA differs from the classical Viterbi algorithm in that it uses a modified path metric which takes into account the a priori probabilities of the input symbols, and produces a soft output indicating the reliability of the decision.

The first step in the SOVA is the selection of the survivor path, passing through one unique node at each time instant, t. Since each node has 2 branches converging at it (with one branch being chosen to form the Survivor Path, and the other being discarded), the difference in the branch metrics (or cost) between the chosen and discarded branches indicate the amount of error in the choice.

This cost is accumulated over the entire sliding window (usually equals at least five constraint lengths), to indicate the soft output measure of reliability of the hard bit decision of the Viterbi algorithm.

See also

• Expectation–maximization algorithm
• Baum–Welch algorithm
• Forward-backward algorithm
• Forward algorithm
• Error-correcting code
• Viterbi decoder
• Hidden Markov model
• Part-of-speech tagging
• A* search algorithm

General references

• Viterbi AJ (April 1967). "Error bounds for convolutional codes and an asymptotically optimum decoding algorithm". IEEE Transactions on Information Theory 13 (2): 260–269. doi:10.1109/TIT.1967.1054010.  (note: the Viterbi decoding algorithm is described in section IV.) Subscription required.
• "A fast maximum-likelihood decoder for convolutional codes". Proceedings IEEE 56th Vehicular Technology Conference. 1. 2002. pp. 371–375. doi:10.1109/VETECF.2002.1040367. ISBN 978-0-7803-7467-6. 
• Forney GD (March 1973). "The Viterbi algorithm". Proceedings of the IEEE 61 (3): 268–278. doi:10.1109/PROC.1973.9030.  Subscription required.
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 16.2. Viterbi Decoding". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=850. 
• Rabiner LR (February 1989). "A tutorial on hidden Markov models and selected applications in speech recognition". Proceedings of the IEEE 77 (2): 257–286. doi:10.1109/5.18626.  (Describes the forward algorithm and Viterbi algorithm for HMMs).
• Shinghal, R. and Godfried T. Toussaint, "Experiments in text recognition with the modified Viterbi algorithm," IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. PAMI-l, April 1979, pp. 184–193.
• Shinghal, R. and Godfried T. Toussaint, "The sensitivity of the modified Viterbi algorithm to the source statistics," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-2, March 1980, pp. 181–185.

External links

• Implementations in Java, F#, Clojure, C# on Wikibooks
• Tutorial on convolutional coding with viterbi decoding, by Chip Fleming
• A tutorial for a Hidden Markov Model toolkit (implemented in C) that contains a description of the Viterbi algorithm
• Viterbi algorithm by Dr. Andrew J. Viterbi (scholarpedia.org).

Implementations

• Mathematica has an implementation as part of its support for stochastic processes
• Susa signal processing framework provides the C++ implementation for Forward error correction codes and channel equalization here.
• C++
• C#
• Java
• Java 8
• Julia (HMMBase.jl)
• Perl
• Prolog
• Haskell
• Go
• SFIHMM includes code for Viterbi decoding.